 This post was contributed by ISAK mathematics teacher, Mr. Benoit Lachance. Mr. Lachance loves teaching mathematics and constantly strives to enhance his students’ appreciation of mathematical ideas while bringing real-world applications for mathematics into the classroom.
This post was contributed by ISAK mathematics teacher, Mr. Benoit Lachance. Mr. Lachance loves teaching mathematics and constantly strives to enhance his students’ appreciation of mathematical ideas while bringing real-world applications for mathematics into the classroom.
Designing a Sports Field Using a Quadratic Function
Pure math or applied math? What’s your preference? Providing the right balance between the two lies at the heart of any mathematics curriculum. So it’s always a treat for me when the opportunity presents itself to challenge my students to transfer their skills and knowledge in abstract algebra to a practical real-world situation.
The topic we have been studying for several weeks is quadratic functions. Here in Japan, quadratic functions are one of the four broad topics that define the MEXT (Monbu Kagaku Sho) curriculum for Grade 10 students. We spent a few weeks mastering the skills, solving the equations, drawing the graphs, and learning a variety of ‘tools’ to solve problems.
Next it was time to see how well we could use the tools to solve a practical question:
 What are the ideal dimensions for a soccer field and 400 meter running track, or more precisely stated, what are the dimensions of the largest rectangular field that will fit inside an oval with a 400m perimeter?
What are the ideal dimensions for a soccer field and 400 meter running track, or more precisely stated, what are the dimensions of the largest rectangular field that will fit inside an oval with a 400m perimeter?
As with many mathematical problems, the simplicity of the question belies the difficulty of arriving at a solution. The key was for students to create their own mathematical function, an equation in which all the possible choices can be revealed through just one chosen variable.
Here is one possible function:
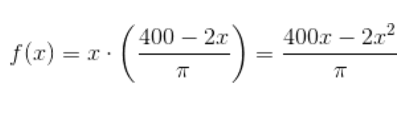 Next, the students needed to arrive at a value of “x” that makes the expression as large as possible. Recognizing the expression as a quadratic function, my students quickly realized the solution would be equivalent to the vertex point of the graph!
Next, the students needed to arrive at a value of “x” that makes the expression as large as possible. Recognizing the expression as a quadratic function, my students quickly realized the solution would be equivalent to the vertex point of the graph!

At the very end of the process, we used a calculator to approximate the exact answer: 100m by 63.7m, or a field of 6370 square meters.
To complete the project, we did a little online research to look up the size of various well-known soccer fields and were surprised to learn that larger fields are theoretically possible! How can this be? It is a salutary reminder that models can only be as good as the assumptions we make to construct them. In this instance, we deduced that the invisible center point of the semi-circles of the track can be moved away from the goal line to expand the field ever so slightly. Our answer was not ‘wrong’, but it could be modified if we choose to reconsider our assumptions.
A challenge for another day!






